A perfect number is a positive integer that is equal to the sum of its proper divisors, excluding itself. Proper divisors of a number are all the divisors excluding the number itself.
For example, let’s take 6, which is the smallest perfect number:
- The divisors of 6 are 1, 2, 3, and 6.
- If we exclude 6 itself, the proper divisors are 1, 2, and 3.
- The sum of these divisors is 1 + 2 + 3 = 6, which is equal to the number itself.
Hence, 6 is a perfect number.
Perfect numbers have been studied for centuries and have interesting properties and connections to other areas of mathematics, such as Mersenne primes. Every even perfect number can be expressed in the form:
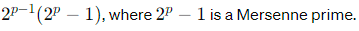
However, it is still unknown whether there are any odd perfect numbers, as none have been found to date.
Here are the first ten perfect numbers, which correspond to the first ten Mersenne primes:
- First Perfect Number: 6
- Second Perfect Number: 28
- Third Perfect Number: 496
- Fourth Perfect Number: 8,128
- Fifth Perfect Number: 33,550,336
- Sixth Perfect Number: 8,589,869,056
- Seventh Perfect Number: 137,438,691,328
- Eighth Perfect Number: 2,305,843,008,139,952,128
- Ninth Perfect Number: 2,658,455,991,569,831,744,654,692,615,953,842,176
- Tenth Perfect Number: 191,561,942,608,236,107,294,793,378,084,303,638,130,997,321,548,169,216
These numbers represent a fascinating aspect of number theory, highlighting the unique properties of perfect numbers and their connection to Mersenne primes.
By the time you reach the 8th perfect number, it is already 2,305,843,008,139,952,128, and they grow exponentially larger from there. The size of these numbers reflects the enormity of the task in finding and verifying Mersenne primes, as the process requires significant computational power and is conducted by projects like the Great Internet Mersenne Prime Search (GIMPS).
